FFT-快速傅里叶变换的推导、推广与优化
Part 1 - FFT的基础推导
离散傅里叶变换
这里我们直接快进到离散傅里叶变换
首先,离散傅里叶逆变换为
\[x[n] = \frac{1}{N}\sum_{k=0}^{N-1}X[k]e^{i2\pi kn/N}\]离散傅里叶变换为
\[X[k] = \sum_{n=0}^{N-1}x[n]e^{-i2\pi kn/N}\]引入单位根
\[\omega_N = e^{i2\pi/N}\] \[\omega_N^k = e^{i2\pi k/N}\]有
\[x[n] = \frac{1}{N}\sum_{k=0}^{N-1}X[k]\omega_N^{kn}\] \[X[k] = \sum_{n=0}^{N-1}x[n]\omega_N^{-kn}\]你可能会好奇 $1/N$ 为什么会出现在这里,但其实如果把傅里叶变换的公式带入到离散傅里叶逆变换的公式中,你会发现,$1/N$ 是为了保证逆变换后的结果与原函数相等
FFT
FFT是DFT的一种快速计算方法,它的时间复杂度为$O(N\log N)$,而DFT的时间复杂度为$O(N^2)$,FFT的时间复杂度比DFT的时间复杂度低了一个数量级,这是非常可观的。
FFT 的核心思想是将 DFT 分解为多个重叠的子问题,然后将这些子问题的结果合并起来,得到最终的结果
\[\begin{align*} X[k] &= \sum_{n=0}^{N-1}x[n]\omega_N^{-kn}\\ &= \sum_{n=0}^{N/2-1}x[2n]\omega_N^{-k(2n)} + \omega_N^k\sum_{n=0}^{N/2-1}x[2n+1]\omega_N^{-k(2n+1)}\\ &= \sum_{n=0}^{N/2-1}x[2n]\omega_{N/2}^{-kn} + \omega_N^k\sum_{n=0}^{N/2-1}x[2n+1]\omega_{N/2}^{-kn}\\ \end{align*}\]为方便起见一般记
\[\omega^{-x} = W^{x}\]FFT 的数据单点映射
最为经典的 FFT 算法是 Cooley-Tukey 算法,它将 DFT 分解为两个长度为 $N/2$ 的 DFT,然后将这两个 DFT 的结果合并起来,得到最终的结果
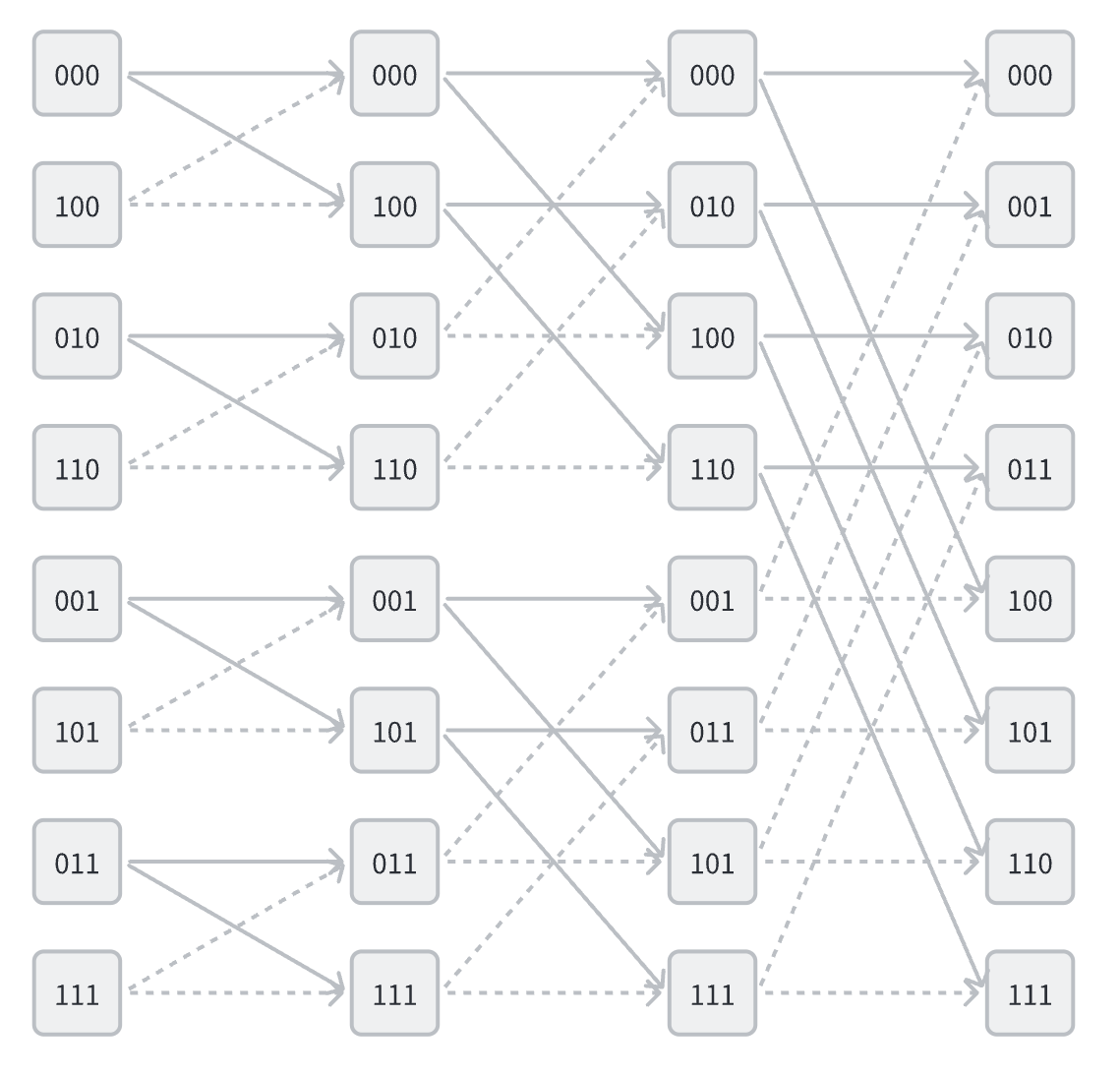
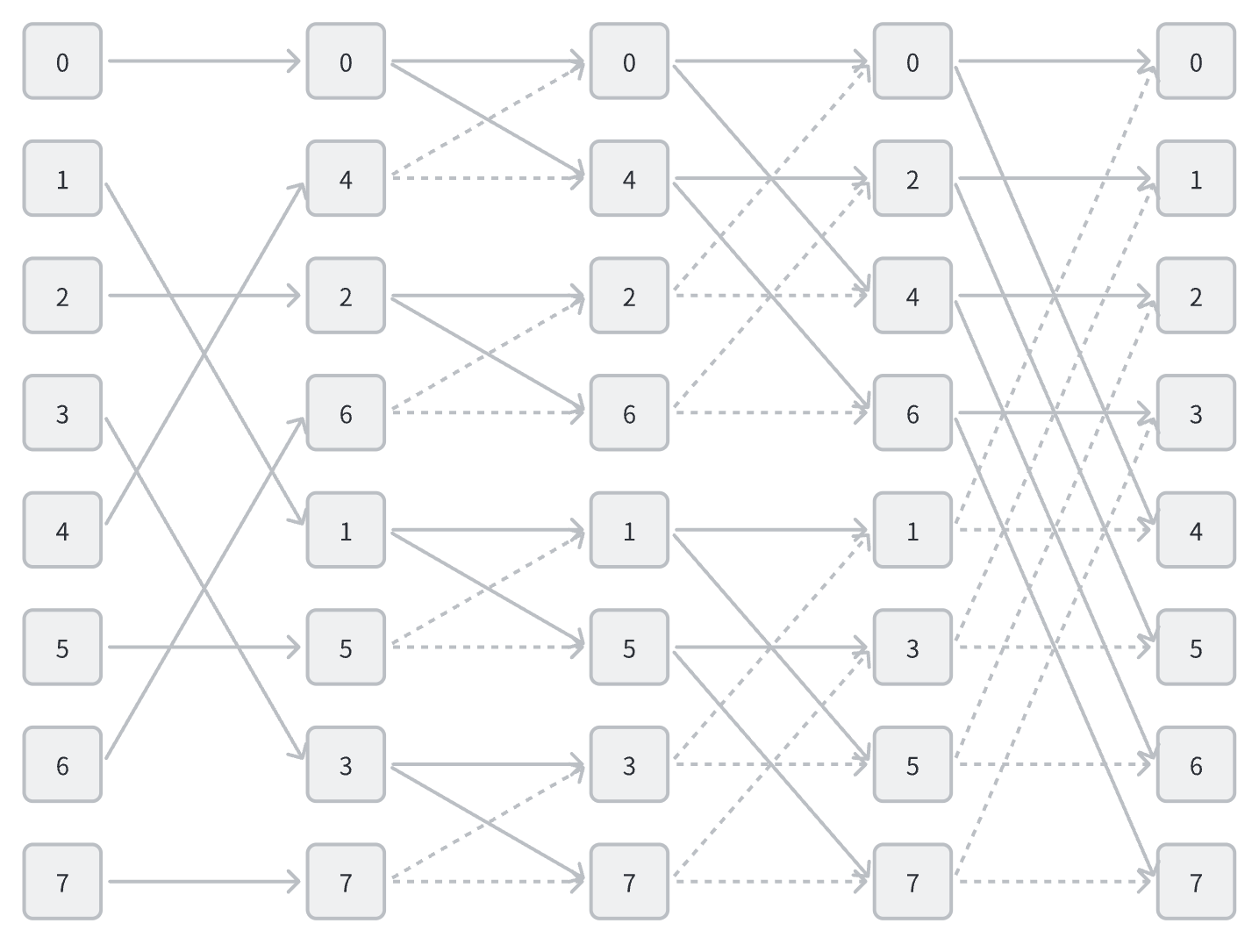
从后向前看,每一层的运算都是将 $N$ 个点分成两组,对于索引来说,这是做了一次逆均匀洗牌 $S^-1$ 即二进制中最低位变成最高位,每一次都进行这样的操作,共进行 $\log_2 N$ 逆均匀洗牌,最后得到的结果就是第一次的编号变成了二进制逆序位,在读入数据时,需要先进行逆序位映射处理,Cooley-Tukey 算法的最终数据映射如下图所示
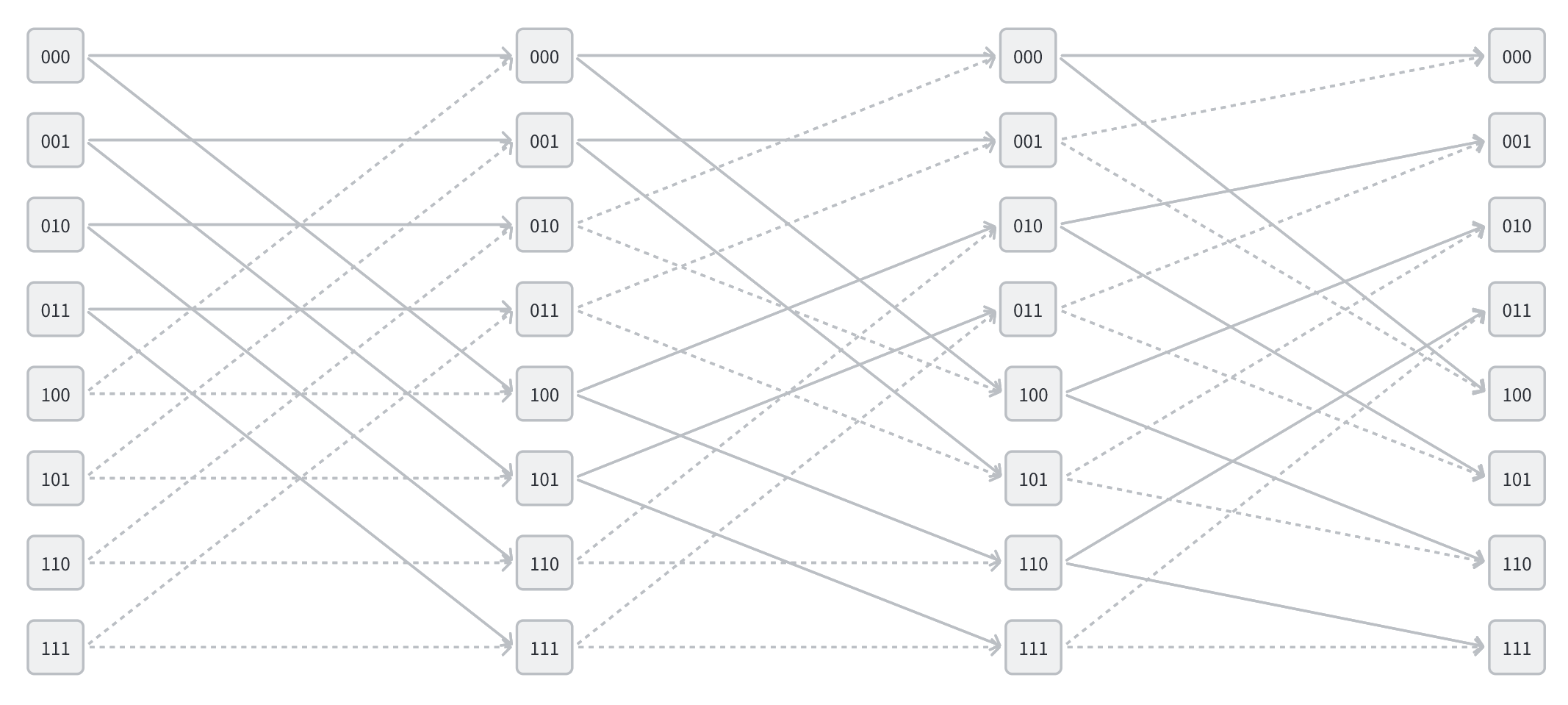
那么有没有不需要进行逆序位映射的方法呢?
如果试着把各层索引进行排序,可以最终得到这样的映射
这样就可以免去逆序位映射这一步操作了,但是相应的代价是需要两倍的空间,因为每一层的一组运算不再是写入到同一组的位置,而是写入到另一组的位置,这样就需要两倍的空间来存储数据。
但是,看这连线图就知道,这个映射不是那么简单,当把连线图做出来的时候,我曾一度怀疑这样的映射是不是真的存在
通过观察连线图来得出这样复杂映射公式是不大可能的,但是通过数学推导可以
我们将 FFT 的递推公式展开,可以得到
\[\begin{align*} X[k] &= \sum_{n=0}^{N/2-1}x[2n]W_{N/2}^{nk} + W_N^k\sum_{n=0}^{N/2-1}x[2n+1]W_{N/2}^{nk}\\ &= \sum_{n=0}^{N/4-1}x[4n]W_{N/4}^{nk} + W_N^k\sum_{n=0}^{N/4-1}x[4n+2]W_{N/4}^{nk} \\&+ W_N^k\left( \sum_{n=0}^{N/4-1}x[4n+1]W_{N/4}^{nk} + W_N^k\sum_{n=0}^{N/4-1}x[4n+3]W_{N/4}^{nk} \right)\\ \end{align*}\]进行一次 FFT 共需要 $L=\log_2N$ 层并行运算,每一层都是将 $N$ 个点分成两组,然后将这两组点合并成一个 $N/2$ 点的DFT
将第 $l$ 层的 $N$ 长度的向量表示为 $X_{N/2^{L-l}}$,那么 $L$ 层为 $X_{N}$ ,第 $L-1$ 层为 $X_{N/2}$, ……,第 $0$ 层为 $X_{N/N} = x$
这里的 $X_{N/2}$ 并不是长度为 $N/2$ 的向量,$X_{N/2}$ 的长度依然为 $N$
这里引入循环数组 $X[k+N]=X[k]$ 因为在傅里叶变换中,数值是周期延拓的,只要在最后进行取模运算即可
根据上面展开的公式,可以得到 在第$\log_2N$ 层的映射关系
\[X_N[k]= X_{N/2}[2k] + W_N^kX_{N/2}[2k+1]\]根据 FFT 的递推公式
\[X[k] = \sum_{n=0}^{N/2-1}x[2n]W_{N/2}^{nk} + W_N^k\sum_{n=0}^{N/2-1}x[2n+1]W_{N/2}^{nk}\]将 $2k$ 中的 $k$ 换元为 $2k$ 与 $2k + 1$
得到在第$L-1$ 层的映射关系
\[\begin{align*} X_{N/2}[2k] &= X_{N/4}[4k] + W_{N/2}^{k}X_{N/4}[4k+2]\\ X_{N/2}[2k+1] &= X_{N/4}[4k+1] + W_{N/2}^{k}X_{N/4}[4k+3]\\ \end{align*}\]将这两个公式翻译一下即:给定在数组 $X_{N/2}$ 中的编号 $k$ , 欲求得 $X_{N/2}[2k]$ ,则需寻 $X_{N/4}$ 中 $4k$ 与 $4k+2$ 的值 ……
再将两条公式合并得到一条公式 先将公式写为分段函数的形式,这里需要将原式中的 $k$ 均换元为 $k’$ 然后分别令 $2k = k’$ $2k+1=k’$ 得到
\[X_{N/2}[k] = \begin{cases} X_{N/4}[2k] + W^{k/2}_{N/2}X_{N/4}[2k+2] & k \text{ mod } 2 = 0\\ X_{N/4}[2k-1] + W^{(k-1)/2}_{N/2}X_{N/4}[2k+1] & k \text{ mod } 2 = 1\\ \end{cases}\]再进行合并
\[X_{N/2}[k] = X_{N/4}[2k - k \text{ mod } 2] +W^{k-k \text{ mod } 2}_{N/2} X_{N/4}[2k + 2 - k \text{ mod } 2]\]继续递推
\[\begin{align*} X_{N/4}[4k] &= X_{N/8}[8k] &+ W^{k}_{N/4}X_{N/8}[8k+4]\\ X_{N/4}[4k+1] &= X_{N/8}[8k+1] &+ W^{k}_{N/4}X_{N/8}[8k+5]\\ X_{N/4}[4k+2] &= X_{N/8}[8k+2] &+ W^{k}_{N/4}X_{N/8}[8k+6]\\ X_{N/4}[4k+3] &= X_{N/8}[8k+3] &+ W^{k}_{N/4}X_{N/8}[8k+7]\\ \end{align*}\]写为分段函数
\[X_{N/4}[k] = \begin{cases} X_{N/8}[2k] + W^{(k )/4}_{N/4}X_{N/8}[2k+4] & k \text{ mod } 4 = 0\\ X_{N/8}[2k-1] + W^{(k-1)/4}_{N/4}X_{N/8}[2k+3] & k \text{ mod } 4 = 1\\ X_{N/8}[2k-2] + W^{(k-2)/4}_{N/4}X_{N/8}[2k+2] & k \text{ mod } 4 = 2\\ X_{N/8}[2k-3] + W^{(k-3)/4}_{N/4}X_{N/8}[2k+1] & k \text{ mod } 4 = 3\\ \end{cases}\]合并
\[X_{N/4}[k] = X_{N/8}[2k - k \text{ mod } 4] + W^{(k-k \text{ mod } 4)/4}_{N/4} X_{N/8}[2k + 4 - k \text{ mod } 4]\]最后可以总结出一般的映射公式
记 $\overline{l} = L- l$ , $\overline{l} \in{ 0,1 ,\cdots,L-1}$
\[X_{N/2^{\overline{l}}}[k] = X_{N/2^{\overline{l}+1}}[2k - k \text{ mod } 2^{\overline{l}}] +W^{(k-k \text{ mod } 2^{\overline{l}})/2^{\overline{l}}}_{N/2^{\overline{l}}} X_{N/2^{\overline{l}+1}}[2k + 2^{\overline{l}} - k \text{ mod } 2^{\overline{l}}]\]鉴于 $X_{N/2^{\overline{l}}}$ 的表述方式过于复杂,且实际计算中也不会出现,记 $X_{N/2^{\overline{l}}}$ 为 $X_{l}$ , 表示在第 $l$ 次 FFT 运算中的写入对象
此外 \(W^{(k-k \text{ mod } 2^{\overline{l}})/2^{\overline{l}}}_{N/2^{\overline{l}}}\) 可以简化为 \(W^{k-k \text{ mod } 2^{\overline{l}}}_{N}\)
上述公式可以简化为
\[X_{l}[k] = X_{l-1}[2k - k \text{ mod } 2^{\overline{l}}] +W^{k-k \text{ mod } 2^{\overline{l}}}_{N} X_{l-1}[2k + 2^{\overline{l}} - k \text{ mod } 2^{\overline{l}}]\]最后进行取模,从循环数组转换到实际计算中的数组
\[X_{l}[k] = X_{l-1}[(2k - k \text{ mod } 2^{\overline{l}})\text{ mod }N] +W^{k-k \text{ mod } 2^{\overline{l}}}_{N/2^{\overline{l}}} X_{l-1}[(2k + 2^{\overline{l}} - k \text{ mod } 2^{\overline{l}})\text{ mod }N]\]其中 $2k - k \text{ mod } 2^{\overline{l}}$ 还有另一种形式的表述
利用 $m \text{ mod } n = m - n \lfloor \frac{m}{n} \rfloor$
\[\begin{align*} 2k - k\text{ mod } 2^{\overline{l}} &= 2k - (k - 2^{\overline{l}}\lfloor \frac{k}{2^{\overline{l}}} \rfloor)\\ &= 2^{\overline{l}}\lfloor \frac{k}{2^{\overline{l}}} \rfloor + k\\ \end{align*}\]在实际的计算中是两次移位运算、一次加法运算,相较 $2k - k \text{ mod } 2^{\overline{l}}$ (一次移位运行、两次加法运算、一次与运算) 更快
同理 $k - k\text{ mod } 2^{\overline{l}} $ 也可以写为 \(\begin{align*} k - k\text{ mod } 2^{\overline{l}} &= 2^{\overline{l}}\lfloor \frac{k}{2^{\overline{l}}} \rfloor\\ \end{align*}\)
下一章中,会讲述如何将其推广到Radix-N的情形