首页 Constraint Satisfaction Problems
文章
取消

Constraint Satisfaction Problems

发表于 2023/04/03 更新于 2023/05/15
作者 Estelle
17 分钟阅读

约束满足问题

约束满足问题的“状态”必须满足若干约束和限制的一组对象，实体表示为对变量进行有限约束的同质集合，通过约束满足方法加以解决

约束满足问题通常呈现出高复杂性，需要将启发式与组合搜索方法相结合

基本概念

  • 变量（Variable）：CSP中需要进行求解的对象，通常用字母或数字来表示，比如X、Y、Z、1、2、3等等。
  • 域（Domain）：变量可以取的所有值的集合。比如在解决数独问题时，每个单元格的域就是1-9。
  • 约束（Constraint）：规定变量取值之间的关系，通常用谓词形式表示，比如 $X + Y = Z$。
  • 解（Solution）：符合约束条件的变量取值集合。即，在给定的约束条件下，所有变量的取值都满足约束条件。
  • 状态（State）：当前的变量取值的集合。
  • 推断（Inference）：根据已有信息进行推断，以便缩小搜索空间。推断通常包括剪枝、约束传播等技术。
  • 搜索空间（Search Space）：指所有可能的变量取值集合的集合，也就是在满足约束条件的前提下，所有可能的解的集合

形式化定义

CSP（约束满足问题）可以被形式化地定义为一个三元组$<X, D, C>$：

  • $X = {x1, x2, …, xn}$ 是一组变量。
  • $D = {D1, D2, …, Dn}$ 是一组域，其中每个域Di包含变量xi可能取的所有值。
  • $C = {C1, C2, …, Cm}$ 是一组约束条件，其中每个约束条件Ci指定了一组关联变量和它们的允许取值的组合$<scope,rel>$。一个约束条件通常被表示为一个谓词，它规定了它所涉及的变量之间的关系。

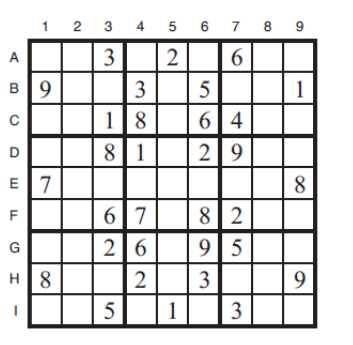
例如在数独中，目的是用数字填满9x9个网格，使得每一行、每一列、以及9个3x3的子网格的每一个都包含从1到9的所有数字

image-20230404170750124

变量

  • 81个格子，每个格子有一个变量
\[X=\begin{pmatrix} A_{1} , A_{2},\dotsc,A_9\newline B_{1} , B_{2},\dotsc,B_9\newline \vdots\newline I_{1} , I_{2},\dotsc,I_9 \end{pmatrix}\]

域

  • 81个变量的取值域为1-9
\[D = (1,2,3,4,5,6,7,8,9)\]

约束

  • 每一行、每一列、每个3x3的子网格(区域)的每一个都包含从1到9的所有数字
\[C = \begin{pmatrix}{} Alldiff (A_1, A_2, …, A_9) , …, Alldiff (I_1, I_2, …, I_9)\newline Alldiff (A_1, B_1, …, I_1) , …, Alldiff (A_9, B_9, …, I_9)\newline Alldiff (A_1, A_2,A_3, …, C_3) , …, Alldiff (G_7,G_8,G_9, …, I_9)\newline \end{pmatrix}\]

一个数独的谜题 (9×9) 和它的谜底

image-20230404181916151

赋值

  1. 定义一个状态空间和解的概念
  2. 每个状态都是通过对变量赋值的形式来定义：${X_i = v_i, X_j = v_j , \dots}$ 赋值的概念
    • 一致性赋值(Consistent assignment):赋值不违反任何约束
    • 完整性赋值(Complete assignment):赋值包含所有变量
    • 局部性赋值(Partial assignment):仅对某些变量赋进行赋值

求解步骤

  1. 定义问题：定义变量、域和约束条件，形成一个CSP问题。
  2. 选择变量：从变量集合中选择一个变量，作为下一步要处理的变量。
  3. 选择取值：从变量的域中选择一个取值，作为当前变量的取值。
  4. 检查约束条件：检查当前变量的取值是否满足所有与之相关的约束条件。如果不满足，则回溯到前一步，选择另一个取值。
  5. 更新变量的域：如果当前变量的取值符合约束条件，则将其更新到与之相关的其他变量的域中，并将这些变量加入到待处理的变量集合中。
  6. 终止条件：重复执行步骤2-5，直到所有变量的取值都被确定或者无法找到可行解为止。

CSP中的常用方法

这里介绍CSP中的三个方法

  • 约束传播
  • 回溯搜索
  • 局部搜索

约束传播

  • 子集合（如变量的子集合）之间的约束关系满足一定的条件
  • 该子集合中的每个变量都有至少一个可行的取值
  • 推断变量的可行值范围，缩小问题的搜索空间

概念：局部一致性(Local Consistency)

局部一致性是CSP中的重要概念，它指的是在某个变量的取值被确定之后，该变量的取值与其他变量的取值之间的关系是否满足约束条件。通过强制局部一致性，我们可以修剪变量的域，这可以加快搜索速度。

局部一致性从弱到强分为三个级别：

  • 节点一致性(Node consistency)

    如果变量的域中所有值满足变量的一元约束，则单个变量（节点）是节点一致的，即每一个变量都在域中

  • 弧一致性(Arc consistency)

    如果域中的每个值满足变量的二元约束，则该变量是弧一致的，即是满足约束图中的每一条边的约束条件

  • 路径一致性(Path consistency)

    对于与 ${X_i, X_j}$ 约束一致的任意赋值 ${X_i = a, X_j = b}$ ，如果存在一个满足对 ${X_i, X_m}$和 ${X_m, X_j}$ 约束的$X_m$赋值，则二元变量集 ${X_i, X_j}$ 对于第三个变量$X_m$是路径一致的

    $X_m$看起来像是一条从$X_i$到$X_j$的路径

    !Generated by ChatGPT!

    In path consistency, we look at the transitive closure of binary constraints in the CSP. That is, we consider all paths of length greater than one in the constraint graph, and we ensure that every value in the domain of a variable can be extended to a consistent assignment with respect to all other variables. If a value cannot be extended, it is pruned from the domain.

    Path consistency is stronger than arc consistency because it considers longer paths in the constraint graph. This can lead to more aggressive pruning of values from domains, which can help in finding solutions faster.

    However, path consistency is also more expensive to enforce than arc consistency, because it requires more computations. As a result, path consistency is often used in combination with other techniques, such as arc consistency or domain consistency, to achieve a good balance between pruning power and computational cost.

  • k一致性(k-consistency)

    上述的三个一致性可以被归纳为k一致性的传播形式

    对于任意 $k - 1$ 个变量的集合以及对于这些变量的任意一致性赋值，如果某个一致性值总是能够被赋值于任意第 $k$ 个变量，则该CSP是k一致性的

    k一致性的概念更强的传播形式

    k一致性的特点

    • $k=1 \iff NodeConsistency$
    • $k=2 \iff ArcConsistency$
    • $k=3 \iff PathConsistency$

最流行的约束传播方法是AC-3算法，它支持弧一致性

!Generated by ChatGPT!

AC-3 (Arc Consistency algorithm #3) is an algorithm for enforcing arc consistency in Constraint Satisfaction Problems (CSPs). It is one of the most widely used algorithms for enforcing local consistency in CSPs.

The AC-3 algorithm operates on a CSP with a set of variables, a set of domains, and a set of binary constraints. The goal of the algorithm is to prune values from the domains of variables that cannot be part of any solution to the CSP.

The AC-3 algorithm works by maintaining a queue of arcs (pairs of variables) to be processed. Initially, the queue contains all arcs in the constraint graph. At each step, the algorithm removes an arc from the queue, and checks if the domain of the first variable can be reduced by removing values that are inconsistent with the domain of the second variable. If the domain of the first variable is reduced, the algorithm adds all arcs involving the first variable (except the current arc) back to the queue, to ensure that all constraints are rechecked.

The algorithm terminates when the queue is empty, or when all domains are arc-consistent. If the algorithm terminates with any empty domains, it means that the CSP has no solution.

The AC-3 algorithm is a sound and complete algorithm for enforcing arc consistency. It is sound because it guarantees that every solution to the CSP is an arc-consistent solution, and it is complete because it can detect when the CSP has no solution. However, the AC-3 algorithm is not always the most efficient algorithm for enforcing arc consistency, especially for large or complex CSPs. Other algorithms, such as AC-4 and AC-5, have been proposed to address some of the limitations of AC-3.

回溯搜索

回溯搜索是一种深度优先搜索的通用算法，用于查找某些计算问题的答案 回溯搜索递增地构建解的候选，而且一旦确定部分候选c不能成为一个合法的解，就将c抛弃(回溯) 回溯搜索的两种改进

  1. 变量赋值可交换，例如$[WA = red , NT = green] \iff [NT = green , WA = red]$
  2. 检查所需的约束
    • 仅需考虑与前面赋值不发生冲突的值
    • 也许需要检查该约束。递增式目标检测

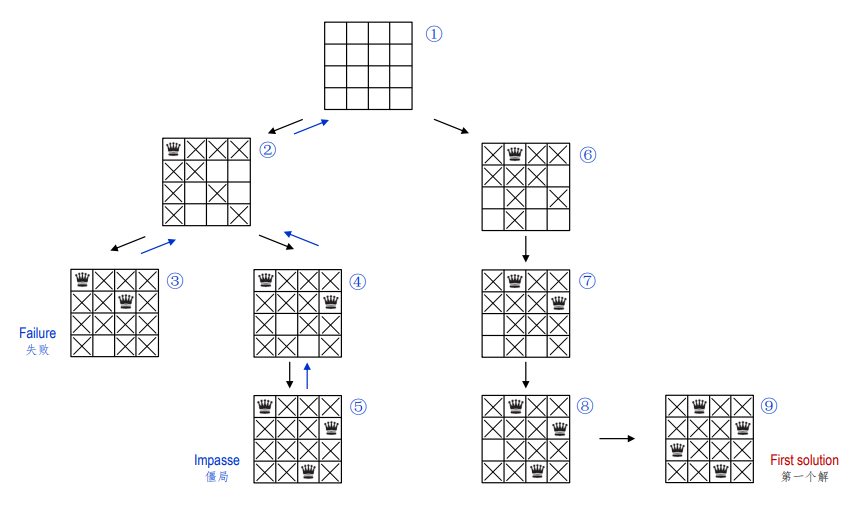
例如8皇后难题：在棋盘的在前k行上布局k个皇后，所有这些要在不同的行与列上

若将8皇后难题简化为4皇后问题，回溯的过程将如下图所示

image-20230404154814702.png

变量与值的排序

合适的启发策略可以加速CSP的求解过程

  • 最小剩余值(Minimum-remaining-values) 选择具有最少“合法”值的变量，也被称为“最受约束变量”
  • 度启发式(Degree heuristic) 选择与未赋值的变量约束最大的变量（度最大），来减少未来选择的分支因子，即“最重要变量”
  • 最少约束值启发式(Least-Constraining-Values heuristic) 尽量选取能排除约束图中相邻变量最少选择的值，即是对CSP的棘手问题优先解决

推理

在每一次选择变量的取值后，预处理约束条件，去除不合法的取值，从而减少搜索空间。推理使得变量均满足弧一致性

局部搜索

局部搜索是一种近似算法（Approximate algorithms），是一种简单的贪心搜索算法，算法每次从当前解的邻域解空间中选择一个最好邻居作为下次迭代的当前解，直到达到一个局部最优解(local optimal solution)

局部搜索算法在求解许多CSPs问题中也很有效

  • 初始状态：为每个变量赋值
  • 搜索：一次改变一个变量的值

局部搜索下有两种常见的启发式

  1. 最小冲突启发式(Min-conflicts Heuristic)

    变量选择：随机选择任意一个冲突变量 值的选择：选择导致与其它变量呈现最少冲突的新值

  2. 约束加权(Constraint Weighting)

    加权约束能聚焦于重要的约束，对高原增加了地势，确保能够改善当前的状态，对证明难以求解的约束也增加权重

    1. 给定每个约束一个数值权重，$W_i$，初始值都为1
    2. 每一步，选择一个变量/值对加以改变，这将导致所有违反约束的总权重为最低
    3. 通过增加当前分配所违反的每个约束的权重来调整权重

将问题转化为CSP

CSP是对很多种问题的一种自然表示，与其它搜索技术相比，CSP求解系统更容易解决问题，CSP求解系统比状态空间搜索更快，因为它可以快速排除大的搜索空间样本

  • 问题分解 ​ 由约束图所表征的问题结构，可以用于寻找解，求解一个CSP问题的复杂性，与约束图的结构密切相关

  • 独立子问题 ​ 独立子问题可被标识为约束图的连通图，即子问题的变量间没有二元或者三元的约束条件 ​ 设$n$个变量的图可分解为仅有$c$个变量的子问题 ​ 每个最坏解的代价是$O((\frac{n}{c})\cdot d^c)$，$n$的线性关系，如果不分解，则总的运行是$O(d^n)$

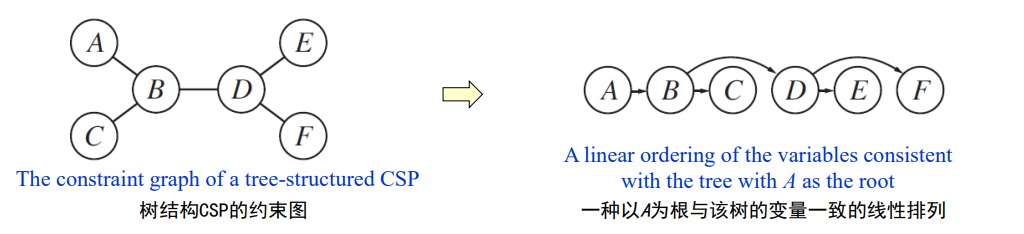
  • 树结构问题 任何树结构的CSP都可以用变量数中的时间线性加以解决,求解树结构CSP的方法：先挑选任意变量作为树的根，然后再选择一个排列（称为拓扑排序），对于一个树结构的CSP，可以在$O(n·d^2 )$时间内得到解

image-20230404213327528

  • 简化约束图为树结构

割集调节(Cutset Conditioning)

调节：对一个变量进行实例化，剪去它的相邻范畴, 可以将一个通用CSP问题简化为一个树结构CSP，并且若能够找到一个小割集则相当有效

image-20230404214920840

树分解(Tree Decomposition) 这种技法将CSP转换成一棵子问题树，并且当该约束图的树宽较小时很有效

image-20230404214905197

markdown, AI, Algorithm
AI Algorithm
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容